tanx的泰勒展开式:
tanx=x+x^3/3+(2 x^5)/15+(17 x^7)/315+(62 x^9)/2835+O[x]^11(|x|<π/2)。
常用泰勒展开式
1、e^x = 1+x+x^2/2!+x^3/3!+……+x^n/n!+……
2、ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k + ……(|x|<1)

3、sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞<x<∞),
4、cos x = 1-x^2/2!+x^4/4!-……+(-1)k*(x^(2k))/(2k)!+…… (-∞<x<∞),
5、arcsin x = x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + ……(|x|<1),
6、arccos x = π - ( x + 1/2*x^3/3 + 1*3/(2*4)*x^5/5 + …… ) (|x|<1),
7、sinh x = x+x^3/3!+x^5/5!+……+(-1)^(k-1)*(x^2k-1)/(2k-1)!+…… (-∞<x<∞)
独缺tanx 泰勒展开式。有好事者用sinx/cosx算出 tanx 泰勒展开式的前五项。
tanx=x+x^3/3+(2 x^5)/15+(17 x^7)/315+(62 x^9)/2835+O[x]^11
最后一项是余项,(|x|<π/2).
方法就是多项式的 竖式除法 ,只不过是把低次幂排在前面。

当|x|<π/4时,舍弃余项,误差较小。
当x=π/4时, tanx=1,无须tanx 泰勒展开式。
当π/41,误差很大。
这种情况要转换思路,令y=π/2-x,用10阶泰勒展开式算出tany,
然后 tanx=1/tany
同理,当-π/2
然后 tanx=1/tany
所以, 当x=π/4时, tanx泰勒展开式误差最大。
10阶五项 tan(π/4)=0.99917,误差8.3/10000
6阶三项 tan(π/4)=0.9867,误差 >1%
直接用sinx,cosx的泰勒展开式相除,分别取前三项
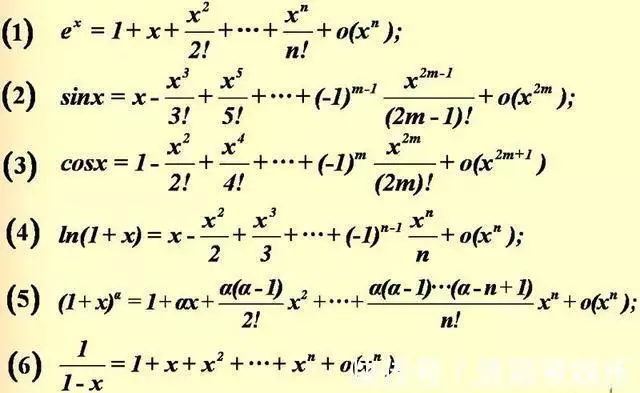
sin(π/4)=0.707143, cos(π/4)=0.707429,
sin(π/4)/ cos(π/4)=0.999595, 误差约4/10000
对比可知,五项tanx的泰勒展开式比三项sinx/cosx的泰勒展开式误差还大,
并且π/4
所以 tanx泰勒展开式不常用。
不过,当 |x|<π/6时,tanx的泰勒展开式的误差还算小 ,可用。
