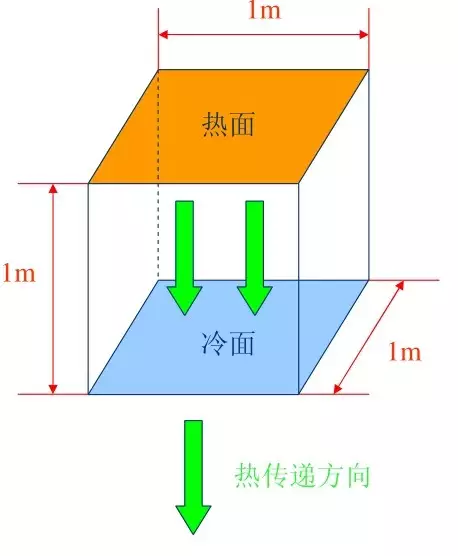
导热系数也叫导热率(thermal conductivity),导热系数是指在稳定传热条件下,1m厚的材料,两侧表面的温差为1度(K,℃),在1秒钟的时间内,通过1平方米面积传递的热量,单位为瓦/米.度(W/m.K,此处的K也可以用℃代替)。是表示材料热传导能力大小的物理量,使用傅立叶定律作为其导热系数的计算公式。
材料的导热系数会随组成成分、物理结构、物质状态、温度、压力等而变化。不同成分的导热率差异较大,导致由不同成分构成的物料的导热率差异较大。空气为热的不良导体,单粒物料的导热性能好于堆积物料。
此外,一般上面我们定义的导热系数是针对均质材料而言的。实际情况下,还存在有多孔、多层、多结构、各向异性材料,此种材料获得的导热系数实际上是一种综合导热性能的表现,也称之为平均导热系数。
傅立叶定律是传热学中的一个基本定律,可以用来计算热量的传导量(Fourier's law of heat conduction)。
那么,导热系数计算公式是什么呢?
根据傅立叶导热定律,相关的导热系数计算公式表达如下:
Φ=-λA(dt/dx)
q=-λ(dt/dx)
其中Φ为导热量,单位为W
λ:导热系数
A:传热面积,单位为㎡
t:温度,单位为K
x:在导热面上的坐标,单位为m
q:沿x方向传递的热流密度(严格地说热流密度是矢量,所以q应是热流密度矢量在x方向的分量)单位为W/㎡
dt/dx:物体沿x方向的温度变化率
一般形式的数学表达式:q=-λgradt=-λ(dt/dx)n
式中:gradt是指空间某点的温度梯度(temperature gradient);n是指通过该点的等温线上的法向单位矢量,指温度升高的方向。
上述式中负号表示传热方向与温度梯度方向相反
λ表征材料导热性能的物性参数(λ越大,导热性能越好)。
通常,在日常实验中物质的导热性能不能单单利用导热系数计算公式就能简单获得,而需要通过理论和实验相结合方式才是导热系数数据的重要来源方式。
来源:http://www.nfion.com/Article/s16.html
