
费马小定理:
如果p是一个素数,而a是任何不能被p整除的整数,那么p能除aᵖ⁻¹ - 1。
这个由皮埃尔·德·费马在1640年发现的数字性质,本质上是说,取任意素数p和任意不能被该素数整除的数a,假设p = 7, a = 20。通过费马小定理,我们发现:
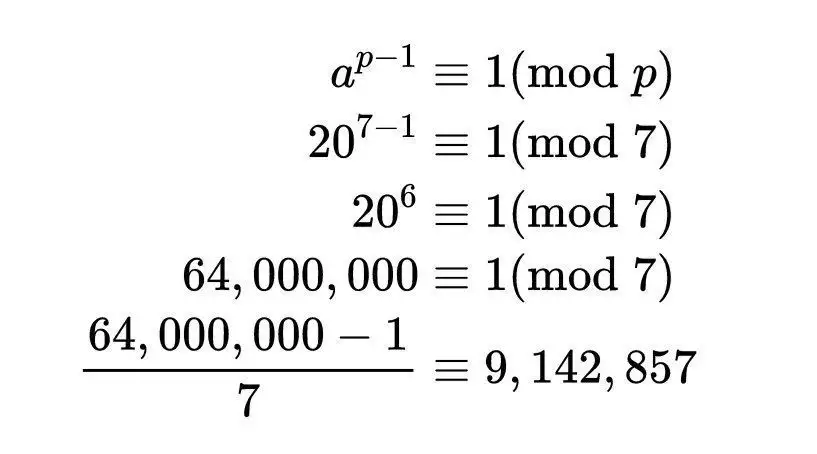
我们不太关心这个计算结果的实际数字。这个定理告诉我们,我们不需要做任何计算就能知道一个整数必须由它得出。
介绍
在17世纪皮埃尔·德·费马与世界各地数学家的许多通信中,与法国铸币局官员伯纳德·弗雷尼卡·德·贝西(1605-1675)的通信对数论影响最大。据说,德·贝西在法国以计算大数的天赋而闻名。

当他听说费马提出了一个寻找立方数的问题,这个立方数的因数加起来就是平方数,就像7³+(1 + 7 + 7²)= 20²一样,贝西立即给出了四个不同的解,第二天又给出了六个。——节选,《初等数论》
德•贝西本人后来最为人所知的是他的著作《寻找等效于魔法格的正方形》(Finding the square equivalent of magic tables),这是他死后于1693年出版的一篇关于魔方格的专著,他在书中提供了880个4阶的魔方格。魔方格是一个n × n的格子,格子里填满了不同的正整数,每个格子里包含一个不同的整数,并且每一行、每一列和每对角线上的整数的和都是相同的。
作为数学家,费马在很多方面都无法与贝西相提并论,但谈到数论家,没有一个同时代的人能挑战费马。费马和贝西在17世纪中期的合作导致了数论中一些最惊人的发现,包括数字1729的立方属性。
然而,两人最引人注目的通信是费马在1640年10月18日的一封信中提出了后来被称为费马小定理的定理。
证明
将近一百年后的1736年,欧拉在圣彼得堡学院学报上发表了一篇题为《关于素数的某些定理的证明》的论文,成为第一个证明费马小定理的人。然而,后来人们发现,莱布尼茨在1683年之前的某个时候,在一份未发表的手稿中给出了几乎相同的证明,但欧拉不可能知道。
今天,这个定理的许多证明已经为人所知。证明一般依赖于两种简化,首先,假设a在0≤a≤p−1范围内。第二,证明费马小定理在1≤a≤p−1范围内成立是充分的。
用二项式定理证明
欧拉的第一个证明是多项式定理的一个非常简单的应用:
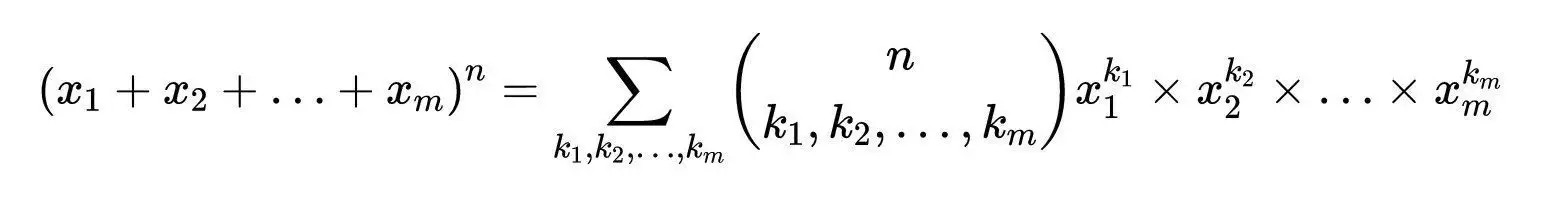
- 多项式定理
这个求和是通过kₐ得到的所有非负整数索引k₁的序列,这样所有kᵢ的和就是n,如果我们把a表示为1的p次方的和(1 + 1+ 1+…1ₐ)ᵖ,我们得到:
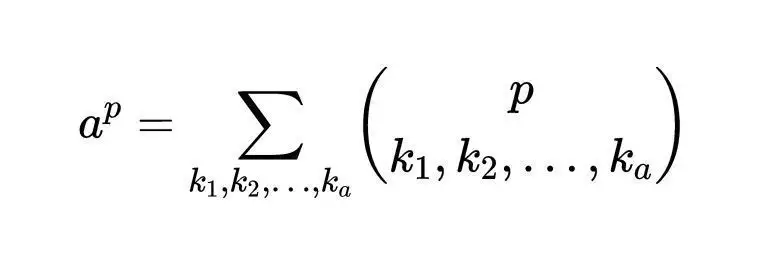
如果p是质数,对于任意j,kⱼ不等于p,我们有:
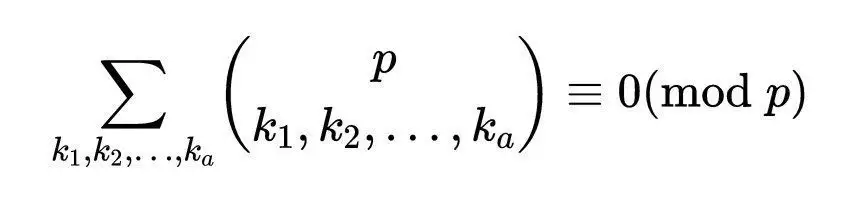
如果p是质数,对于某个j,kⱼ=p,我们有:
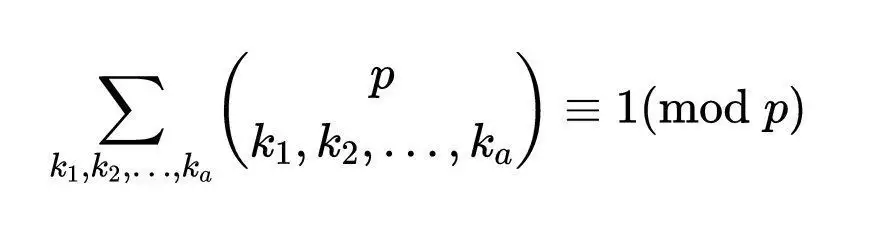
因为正好有一个元素使kⱼ= p,所以定理成立。
作为欧拉定理的一个推论的证明
这个定理的另一个证明是,欧拉定理是费马小定理的推广。欧拉定理指出,若n,a为正整数,且n和a互质,则:
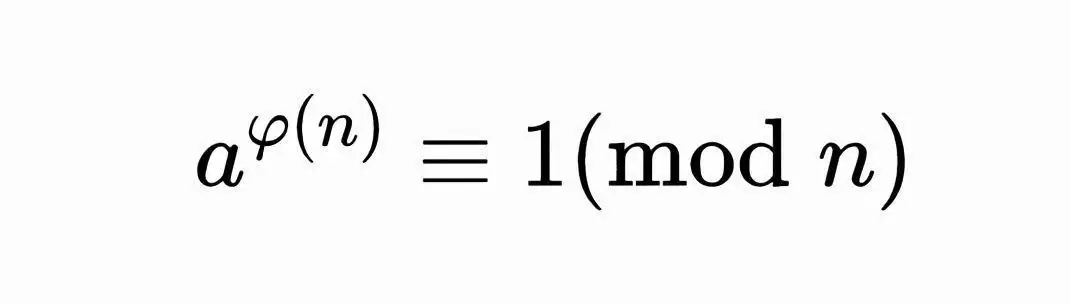
其中φ(n)是欧拉函数,它计算从1到n之间的素数。如果n是素数,则得出费马小定理,即φ(n) = n−1。费马小定理的证明可以从欧拉定理的证明中得到,欧拉定理的证明通常是用群论来完成的。
模算法证明
下面的证明,使用模运算,最初是由James Ivory在1806年发现的,后来被Dirichlet在1828年重新发现。
费马小定理的证明
我们首先考虑整数a,2a,3a,…(p - 1)a。这些数都不等于p对其他数的模,也不等于0。如果这样,那么有:
r × a ≡ s × a (mod p),1 ≤ r
那么,两边消去a将得到r≡s (mod p),这是不可能的,因为r和s都在1和p - 1之间。因此,前一组整数必须同余模p到1,2,…p - 1。把这些同余相乘,你会发现:
a × 2a × 3a × ... × (p - 1) × a ≡ 1 × 2 × 3 × ... × (p - 1)(mod p)
意味着
aᵖ⁻¹ × (p - 1)! ≡ (p - 1)!(mod p)。
从这个表达式的两边消去(p - 1)!,我们得到:
aᵖ⁻¹ ≡ 1 (mod p)。
用群论证明
用群论证明费马小定理,考虑到集合G ={1,2,…,p−1}用乘法运算形成一个群。在四个群公理中,唯一需要验证的是第四个公理,即G中的元素是可逆的。想了解详细 内容可以看这篇文章:由浅入深,轻松理解抽象代数的重要分支——群论
如果我们假设G中的每个元素都是可逆的,假设a在1≤a≤p−1的范围内,也就是说,假设a是G的一个元素。设k是a的阶数,即使aᵏ≡1 (mod p)为真时的最小正整数。然后数字1,a,a²,…,aᵏ⁻¹ 约模p,形成G的一个序为k的子群,根据拉格朗日定理,k能整除G的阶数,即p−1。对于正整数m,有p−1 = km,并且:
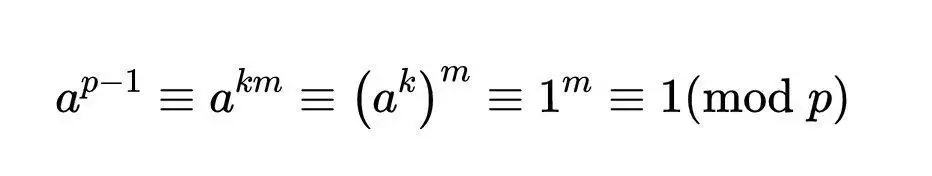
为了证明G与p互质的每个元素b都是可逆的,这个恒等式可以帮助我们如下。因为b和p是素数,贝祖恒等式保证了有整数c和d使得bc + pd = 1。对p取模,这意味着c是b的逆,因为bc≡1(mod p)。因为b是可逆的,所以G中的其他元素也是可逆的,所以G必须是一个群。
应用,素性测试
费马小定理将成为费马质数检验的基础,这是一种确定一个数是否为质数的概率方法。例如,如果我们想知道n = 19是否为素数,随机取 1 < a < 19,假设a = 2。计算n−1 = 18,及其因子是9和6。我们通过计算2¹⁸ ≡ 1 (mod 19), 2⁹ ≡ 18(mod 19)和 2⁶ ≡ 7 (mod 19)来检验,最后发现19必须是素数。
